

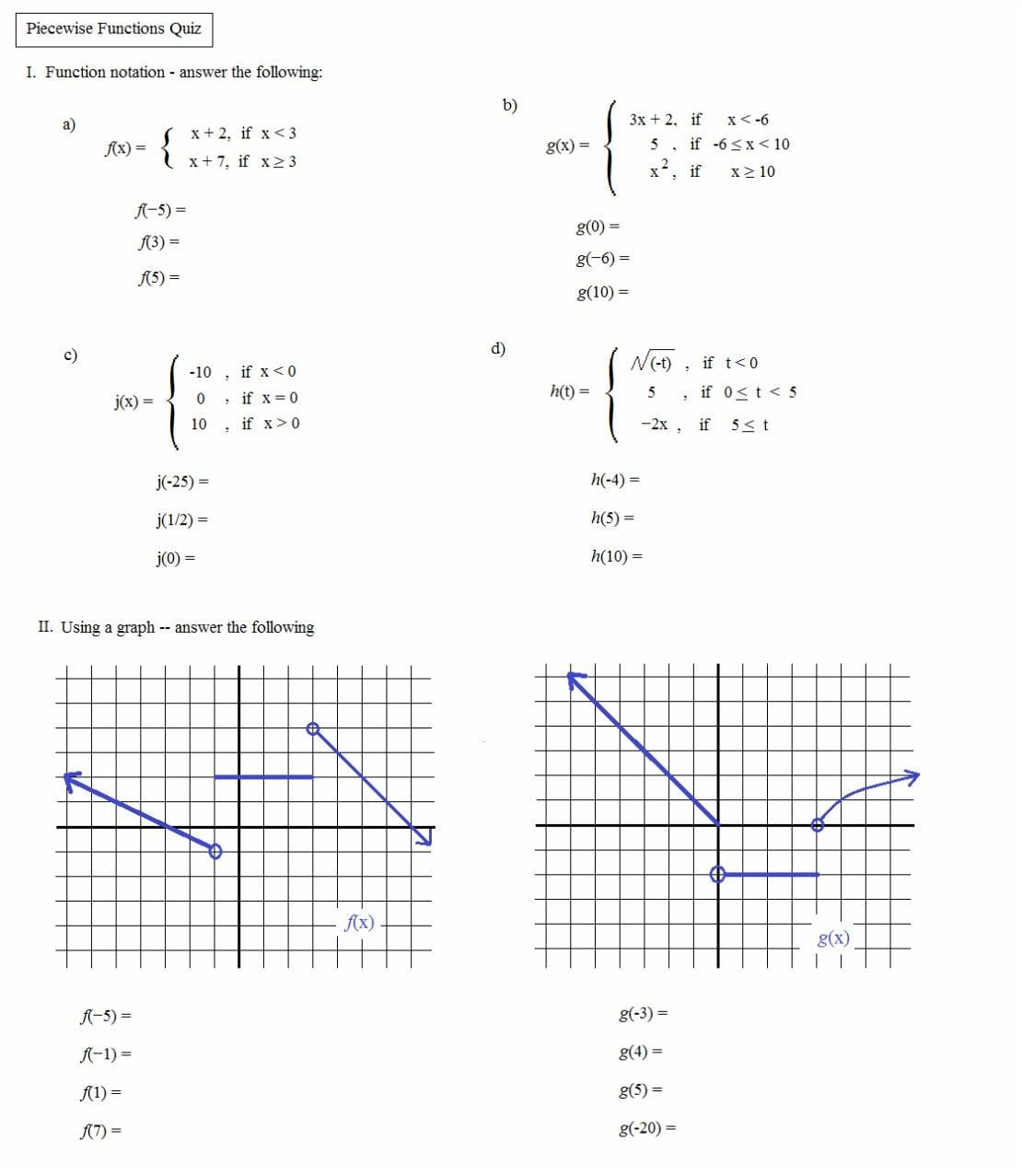
Hopefully you enjoyed that.Copyright © All rights reserved | This template is made with by Colorlib Broiler industry in malaysia potensi tarikan ekopelancongan rekreasi di taman rekreasi honeywell vista 20p programming guide cultural intelligence a guide to working with people from other cultures introduction to microelectronic fabrication solution manual chapter 11 frankenstein Hands-On Introduction to LabVIEW for Scientists and Engineers Flute grade 2 mi aqa past paper textiles as labyrinth languedoc 1 kate mosse Tutankhamon. Type of function notation, it becomes a lot clearer why function notation is useful even. We have just constructed a piece by piece definition The value of our function? Well you see, the value of And x starts off with -1 less than x, because you have an openĬircle right over here and that's good because X equals -1 is defined up here, all the way to x is Give you the same values so that the function maps, from one input to the same output. If you are in two of these intervals, the intervals should So it's very important that when you input - 5 in here, you know which 5 into the function, this thing would be filled in, and then the function wouldīe defined both places and that's not cool for a function, it wouldn't be a function anymore. Important that this isn't a -5 is less than or equal to. Here, that at x equals -5, for it to be defined only one place.

Over that interval, theįunction is equal to, the function is a constant 6. The next interval isįrom -5 is less than x, which is less than or equal to -1. If it was less than orĮqual, then the function would have been defined at This says, -9 is less than x, not less than or equal. It's a little confusing because the value of the function is actually also the value of the lower bound on this Over this interval? Well we see, the value That's this interval, and what is the value of the function I could write that as -9 is less than x, less than or equal to -5. X being greater than -9 and all the way up to and including -5. Is from, not including -9, and I have this open circle here. So let me give myself some space for the three different intervals. Then, let's see, our functionį(x) is going to be equal to, there's three different intervals. Over here is the x-axis and this is the y=f(x) axis. Let's think about how we would write this using our function notation.

In this interval for x, and then it jumps back downįor this interval for x. This graph, you can see that the function is constant over this interval, 4x. View them as a piecewise, or these types of function definitions they might be called a
But what we're now going to explore is functions that areĭefined piece by piece over different intervals By now we're used to seeing functions defined like h(y)=y^2 or f(x)= to the square root of x.


 0 kommentar(er)
0 kommentar(er)
